Journal Description
Tomography
Tomography
is an international, peer-reviewed open access journal on imaging technologies published monthly online by MDPI (from Volume 7 Issue 1-2021).
- Open Access— free for readers, with article processing charges (APC) paid by authors or their institutions.
- High Visibility: indexed within Scopus, SCIE (Web of Science), PubMed, MEDLINE, PMC, and other databases.
- Journal Rank: CiteScore - Q2 (Radiology, Nuclear Medicine and Imaging)
- Rapid Publication: manuscripts are peer-reviewed and a first decision is provided to authors approximately 24.5 days after submission; acceptance to publication is undertaken in 2.8 days (median values for papers published in this journal in the second half of 2023).
- Recognition of Reviewers: APC discount vouchers, optional signed peer review, and reviewer names published annually in the journal.
Impact Factor:
1.9 (2022);
5-Year Impact Factor:
2.2 (2022)
Latest Articles
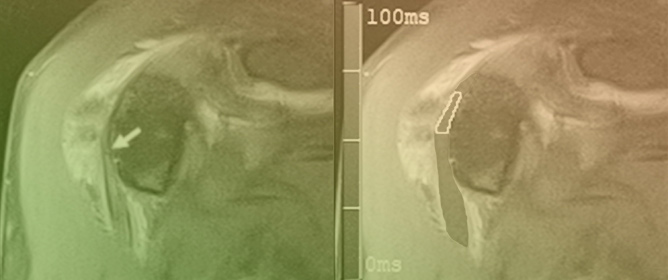
Advanced Imaging of Shunt Valves in Cranial CT Scans with Photon-Counting Scanner
Tomography 2024, 10(5), 654-659; https://doi.org/10.3390/tomography10050050 (registering DOI) - 25 Apr 2024
Abstract
This brief report aimed to show the utility of photon-counting technology alongside standard cranial imaging protocols for visualizing shunt valves in a patient’s cranial computed tomography scan. Photon-counting CT scans with cranial protocols were retrospectively surveyed and four types of shunt valves were
[...] Read more.
This brief report aimed to show the utility of photon-counting technology alongside standard cranial imaging protocols for visualizing shunt valves in a patient’s cranial computed tomography scan. Photon-counting CT scans with cranial protocols were retrospectively surveyed and four types of shunt valves were encountered: proGAV 2.0®, M.blue®, Codman Certas®, and proSA®. These scans were compared with those obtained from non-photon-counting scanners at different time points for the same patients. The analysis of these findings demonstrated the usefulness of photon-counting technology for the clear and precise visualization of shunt valves without any additional radiation or special reconstruction patterns. The enhanced utility of photon-counting is highlighted by providing superior spatial resolution compared to other CT detectors. This technology facilitates a more accurate characterization of shunt valves and may support the detection of subtle abnormalities and a precise assessment of shunt valves.
Full article
(This article belongs to the Section Neuroimaging)
►
Show Figures
Open AccessArticle
Optimizing CT Abdomen–Pelvis Scan Radiation Dose: Examining the Role of Body Metrics (Waist Circumference, Hip Circumference, Abdominal Fat, and Body Mass Index) in Dose Efficiency
by
Huda I. Almohammed, Wiam Elshami, Zuhal Y. Hamd and Mohamed Abuzaid
Tomography 2024, 10(5), 643-653; https://doi.org/10.3390/tomography10050049 (registering DOI) - 24 Apr 2024
Abstract
►▼
Show Figures
Objective: This study investigates the correlation between patient body metrics and radiation dose in abdominopelvic CT scans, aiming to identify significant predictors of radiation exposure. Methods: Employing a cross-sectional analysis of patient data, including BMI, abdominal fat, waist, abdomen, and hip circumference,
[...] Read more.
Objective: This study investigates the correlation between patient body metrics and radiation dose in abdominopelvic CT scans, aiming to identify significant predictors of radiation exposure. Methods: Employing a cross-sectional analysis of patient data, including BMI, abdominal fat, waist, abdomen, and hip circumference, we analyzed their relationship with the following dose metrics: the CTDIvol, DLP, and SSDE. Results: Results from the analysis of various body measurements revealed that BMI, abdominal fat, and waist circumference are strongly correlated with increased radiation doses. Notably, the SSDE, as a more patient-centric dose metric, showed significant positive correlations, especially with waist circumference, suggesting its potential as a key predictor for optimizing radiation doses. Conclusions: The findings suggest that incorporating patient-specific body metrics into CT dosimetry could enhance personalized care and radiation safety. Conclusively, this study highlights the necessity for tailored imaging protocols based on individual body metrics to optimize radiation exposure, encouraging further research into predictive models and the integration of these metrics into clinical practice for improved patient management.
Full article
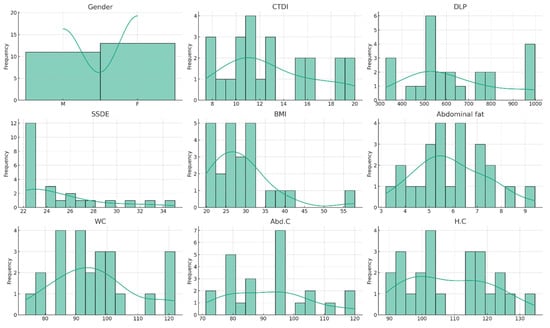
Figure 1
Open AccessArticle
The Additional Role of F18-FDG PET/CT in Characterizing MRI-Diagnosed Tumor Deposits in Locally Advanced Rectal Cancer
by
Mark J. Roef, Kim van den Berg, Harm J. T. Rutten, Jacobus Burger and Joost Nederend
Tomography 2024, 10(4), 632-642; https://doi.org/10.3390/tomography10040048 - 22 Apr 2024
Abstract
Rationale: F18-FDG PET/CT may be helpful in baseline staging of patients with high-risk LARC presenting with vascular tumor deposits (TDs), in addition to standard pelvic MRI and CT staging. Methods: All patients with locally advanced rectal cancer that had TDs on their baseline
[...] Read more.
Rationale: F18-FDG PET/CT may be helpful in baseline staging of patients with high-risk LARC presenting with vascular tumor deposits (TDs), in addition to standard pelvic MRI and CT staging. Methods: All patients with locally advanced rectal cancer that had TDs on their baseline MRI of the pelvis and had a baseline F18-FDG PET/CT between May 2016 and December 2020 were included in this retrospective study. TDs as well as lymph nodes identified on pelvic MRI were correlated to the corresponding nodular structures on a standard F18-FDG PET/CT, including measurements of nodular SUVmax and SUVmean. In addition, the effects of partial volume and spill-in on SUV measurements were studied. Results: A total number of 62 patients were included, in which 198 TDs were identified as well as 106 lymph nodes (both normal and metastatic). After ruling out partial volume effects and spill-in, 23 nodular structures remained that allowed for reliable measurement of SUVmax: 19 TDs and 4 LNs. The median SUVmax between TDs and LNs was not significantly different (p = 0.096): 4.6 (range 0.8 to 11.3) versus 2.8 (range 1.9 to 3.9). For the median SUVmean, there was a trend towards a significant difference (p = 0.08): 3.9 (range 0.7 to 7.8) versus 2.3 (range 1.5 to 3.4). Most nodular structures showing either an SUVmax or SUVmean ≥ 4 were characterized as TDs on MRI, while only two were characterized as LNs. Conclusions: SUV measurements may help in separating TDs from lymph node metastases or normal lymph nodes in patients with high-risk LARC.
Full article
(This article belongs to the Special Issue Functional and Molecular Imaging of the Abdomen)
►▼
Show Figures
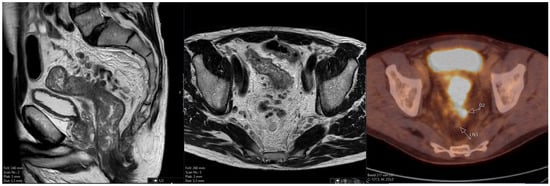
Figure 1
Open AccessArticle
Classification of Osteophytes Occurring in the Lumbar Intervertebral Foramen
by
Abdullah Emre Taçyıldız and Feyza İnceoğlu
Tomography 2024, 10(4), 618-631; https://doi.org/10.3390/tomography10040047 - 19 Apr 2024
Abstract
Background: Surgeons have limited knowledge of the lumbar intervertebral foramina. This study aimed to classify osteophytes in the lumbar intervertebral foramen and to determine their pathoanatomical characteristics, discuss their potential biomechanical effects, and contribute to developing surgical methods. Methods: We conducted a retrospective,
[...] Read more.
Background: Surgeons have limited knowledge of the lumbar intervertebral foramina. This study aimed to classify osteophytes in the lumbar intervertebral foramen and to determine their pathoanatomical characteristics, discuss their potential biomechanical effects, and contribute to developing surgical methods. Methods: We conducted a retrospective, non-randomized, single-center study involving 1224 patients. The gender, age, and anatomical location of the osteophytes in the lumbar intervertebral foramina of the patients were recorded. Results: Two hundred and forty-nine (20.34%) patients had one or more osteophytes in their lumbar 4 and 5 foramina. Of the 4896 foramina, 337 (6.88%) contained different types of osteophytes. Moreover, four anatomical types of osteophytes were found: mixed osteophytes in 181 (3.69%) foramina, osteophytes from the lower endplate of the superior vertebrae in 91 (1.85%) foramina, osteophytes from the junction of the pedicle and lamina of the upper vertebrae in 39 foramina (0.79%), and osteophytes from the upper endplate of the lower vertebrae in 26 (0.53%) foramina. The L4 foramen contained a significantly higher number of osteophytes than the L5 foramen. Osteophyte development increased significantly with age, with no difference between males and females. Conclusions: The findings show that osteophytic extrusions, which alter the natural anatomical structure of the lumbar intervertebral foramina, are common and can narrow the foramen.
Full article
(This article belongs to the Topic AI in Medical Imaging and Image Processing)
►▼
Show Figures
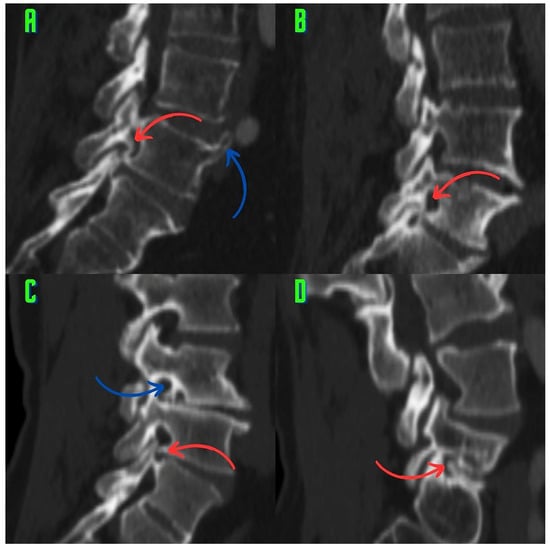
Figure 1
Open AccessCase Report
Executive Functions in a Patient with Low-Grade Glioma of the Central Nervous System: A Case Report
by
Manuel José Guerrero Gómez, Ángela Jiménez Urrego, Fernando Gonzáles and Alejandro Botero Carvajal
Tomography 2024, 10(4), 609-617; https://doi.org/10.3390/tomography10040046 - 18 Apr 2024
Abstract
►▼
Show Figures
Central nervous system tumors produce adverse outcomes in daily life, although low-grade gliomas are rare in adults. In neurological clinics, the state of impairment of executive functions goes unnoticed in the examinations and interviews carried out. For this reason, the objective of this
[...] Read more.
Central nervous system tumors produce adverse outcomes in daily life, although low-grade gliomas are rare in adults. In neurological clinics, the state of impairment of executive functions goes unnoticed in the examinations and interviews carried out. For this reason, the objective of this study was to describe the executive function of a 59-year-old adult neurocancer patient. This study is novel in integrating and demonstrating biological effects and outcomes in performance evaluated by a neuropsychological instrument and psychological interviews. For this purpose, pre- and post-evaluations were carried out of neurological and neuropsychological functioning through neuroimaging techniques (iRM, spectroscopy, electroencephalography), hospital medical history, psychological interviews, and the Wisconsin Card Classification Test (WCST). There was evidence of deterioration in executive performance, as evidenced by the increase in perseverative scores, failure to maintain one’s attitude, and an inability to learn in relation to clinical samples. This information coincides with the evolution of neuroimaging over time. Our case shows that the presence of the tumor is associated with alterations in executive functions that are not very evident in clinical interviews or are explicit in neuropsychological evaluations. In this study, we quantified the degree of impairment of executive functions in a patient with low-grade glioma in a middle-income country where research is scarce.
Full article
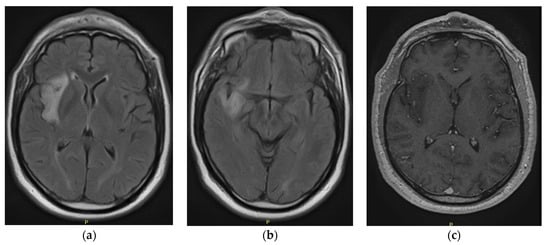
Figure 1
Open AccessReview
Uncommon Causes of Interlobular Septal Thickening on CT Images and Their Distinguishing Features
by
Achala Donuru, Drew A. Torigian and Friedrich Knollmann
Tomography 2024, 10(4), 574-608; https://doi.org/10.3390/tomography10040045 - 17 Apr 2024
Abstract
►▼
Show Figures
Interlobular septa thickening (ILST) is a common and easily recognized feature on computed tomography (CT) images in many lung disorders. ILST thickening can be smooth (most common), nodular, or irregular. Smooth ILST can be seen in pulmonary edema, pulmonary alveolar proteinosis, and lymphangitic
[...] Read more.
Interlobular septa thickening (ILST) is a common and easily recognized feature on computed tomography (CT) images in many lung disorders. ILST thickening can be smooth (most common), nodular, or irregular. Smooth ILST can be seen in pulmonary edema, pulmonary alveolar proteinosis, and lymphangitic spread of tumors. Nodular ILST can be seen in the lymphangitic spread of tumors, sarcoidosis, and silicosis. Irregular ILST is a finding suggestive of interstitial fibrosis, which is a common finding in fibrotic lung diseases, including sarcoidosis and usual interstitial pneumonia. Pulmonary edema and lymphangitic spread of tumors are the commonly encountered causes of ILST. It is important to narrow down the differential diagnosis as much as possible by assessing the appearance and distribution of ILST, as well as other pulmonary and extrapulmonary findings. This review will focus on the CT characterization of the secondary pulmonary lobule and ILST. Various uncommon causes of ILST will be discussed, including infections, interstitial pneumonia, depositional/infiltrative conditions, inhalational disorders, malignancies, congenital/inherited conditions, and iatrogenic causes. Awareness of the imaging appearance and various causes of ILST allows for a systematic approach, which is important for a timely diagnosis. This study highlights the importance of a structured approach to CT scan analysis that considers ILST characteristics, associated findings, and differential diagnostic considerations to facilitate accurate diagnoses.
Full article
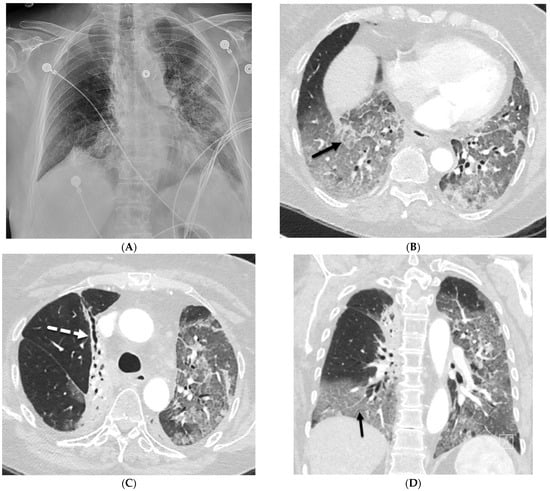
Figure 1
Open AccessReview
Breast Tomographic Ultrasound: The Spectrum from Current Dense Breast Cancer Screenings to Future Theranostic Treatments
by
Peter J. Littrup, Mohammad Mehrmohammadi and Nebojsa Duric
Tomography 2024, 10(4), 554-573; https://doi.org/10.3390/tomography10040044 - 15 Apr 2024
Abstract
►▼
Show Figures
This review provides unique insights to the scientific scope and clinical visions of the inventors and pioneers of the SoftVue breast tomographic ultrasound (BTUS). Their >20-year collaboration produced extensive basic research and technology developments, culminating in SoftVue, which recently received the Food and
[...] Read more.
This review provides unique insights to the scientific scope and clinical visions of the inventors and pioneers of the SoftVue breast tomographic ultrasound (BTUS). Their >20-year collaboration produced extensive basic research and technology developments, culminating in SoftVue, which recently received the Food and Drug Administration’s approval as an adjunct to breast cancer screening in women with dense breasts. SoftVue’s multi-center trial confirmed the diagnostic goals of the tissue characterization and localization of quantitative acoustic tissue differences in 2D and 3D coronal image sequences. SoftVue mass characterizations are also reviewed within the standard cancer risk categories of the Breast Imaging Reporting and Data System. As a quantitative diagnostic modality, SoftVue can also function as a cost-effective platform for artificial intelligence-assisted breast cancer identification. Finally, SoftVue’s quantitative acoustic maps facilitate noninvasive temperature monitoring and a unique form of time-reversed, focused US in a single theranostic device that actually focuses acoustic energy better within the highly scattering breast tissues, allowing for localized hyperthermia, drug delivery, and/or ablation. Women also prefer the comfort of SoftVue over mammograms and will continue to seek out less-invasive breast care, from diagnosis to treatment.
Full article
Figure 1
Open AccessArticle
Three-Dimensional Visualization of Shunt Valves with Photon Counting CT and Comparison to Traditional X-ray in a Simple Phantom Model
by
Anna Klempka, Sven Clausen, Mohamed Ilyes Soltane, Eduardo Ackermann and Christoph Groden
Tomography 2024, 10(4), 543-553; https://doi.org/10.3390/tomography10040043 - 12 Apr 2024
Abstract
This study introduces an application of innovative medical technology, Photon Counting Computer Tomography (PC CT) with novel detectors, for the assessment of shunt valves. PC CT technology offers enhanced visualization capabilities, especially for small structures, and opens up new possibilities for detailed three-dimensional
[...] Read more.
This study introduces an application of innovative medical technology, Photon Counting Computer Tomography (PC CT) with novel detectors, for the assessment of shunt valves. PC CT technology offers enhanced visualization capabilities, especially for small structures, and opens up new possibilities for detailed three-dimensional imaging. Shunt valves are implanted under the skin and redirect excess cerebrospinal fluid, for example, to the abdominal cavity through a catheter. They play a vital role in regulating cerebrospinal fluid drainage in various pathologies, which can lead to hydrocephalus. Accurate imaging of shunt valves is essential to assess the rate of drainage, as their precise adjustment is a requirement for optimal patient care. This study focused on two adjustable shunt valves, the proGAV 2.0® and M. blue® (manufactured by Miethke, Potsdam, Germany). A comprehensive comparative analysis of PC CT and traditional X-ray techniques was conducted to explore this cutting-edge technology and it demonstrated that routine PC CT can efficiently assess shunt valves’ adjustments. This technology shows promise in enhancing the accurate management of shunt valves used in settings where head scans are already frequently required, such as in the treatment of hydrocephalus.
Full article
(This article belongs to the Section Neuroimaging)
►▼
Show Figures

Figure 1
Open AccessArticle
Transcutaneous Ablation of Lung Tissue in a Porcine Model Using Magnetic-Resonance-Guided Focused Ultrasound (MRgFUS)
by
Jack B. Yang, Lauren Powlovich, David Moore, Linda Martin, Braden Miller, Jill Nehrbas, Anant R. Tewari and Jaime Mata
Tomography 2024, 10(4), 533-542; https://doi.org/10.3390/tomography10040042 - 06 Apr 2024
Abstract
►▼
Show Figures
Focused ultrasound (FUS) is a minimally invasive treatment that utilizes high-energy ultrasound waves to thermally ablate tissue. Magnetic resonance imaging (MRI) guidance may be combined with FUS (MRgFUS) to increase its accuracy and has been proposed for lung tumor ablation/debulking. However, the lungs
[...] Read more.
Focused ultrasound (FUS) is a minimally invasive treatment that utilizes high-energy ultrasound waves to thermally ablate tissue. Magnetic resonance imaging (MRI) guidance may be combined with FUS (MRgFUS) to increase its accuracy and has been proposed for lung tumor ablation/debulking. However, the lungs are predominantly filled with air, which attenuates the strength of the FUS beam. This investigation aimed to test the feasibility of a new approach using an intentional lung collapse to reduce the amount of air inside the lung and a controlled hydrothorax to create an acoustic window for transcutaneous MRgFUS lung ablation. Eleven pigs had one lung mechanically ventilated while the other lung underwent a controlled collapse and subsequent hydrothorax of that hemisphere. The MRgFUS lung ablations were then conducted via the intercostal space. All the animals recovered well and remained healthy in the week following the FUS treatment. The location and size of the ablations were confirmed one week post-treatment via MRI, necropsy, and histological analysis. The animals had almost no side effects and the skin burns were completely eliminated after the first two animal studies, following technique refinement. This study introduces a novel methodology of MRgFUS that can be used to treat deep lung parenchyma in a safe and viable manner.
Full article
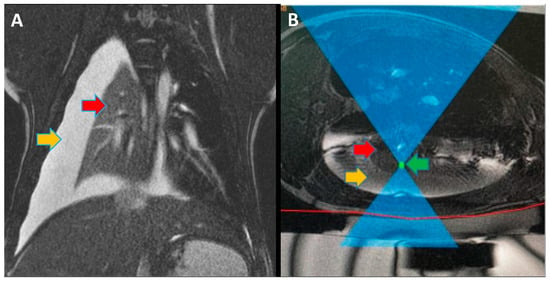
Figure 1
Open AccessArticle
The Value of Ultrasound for Detecting and Following Subclinical Interstitial Lung Disease in Systemic Sclerosis
by
Marwin Gutierrez, Chiara Bertolazzi, Edgar Zozoaga-Velazquez and Denise Clavijo-Cornejo
Tomography 2024, 10(4), 521-532; https://doi.org/10.3390/tomography10040041 - 03 Apr 2024
Abstract
►▼
Show Figures
Background: Interstitial lung disease (ILD) is a complication in patients with systemic sclerosis (SSc). Accurate strategies to identify its presence in early phases are essential. We conducted the study aiming to determine the validity of ultrasound (US) in detecting subclinical ILD in SSc,
[...] Read more.
Background: Interstitial lung disease (ILD) is a complication in patients with systemic sclerosis (SSc). Accurate strategies to identify its presence in early phases are essential. We conducted the study aiming to determine the validity of ultrasound (US) in detecting subclinical ILD in SSc, and to ascertain its potential in determining the disease progression. Methods: 133 patients without respiratory symptoms and 133 healthy controls were included. Borg scale, Rodnan skin score (RSS), auscultation, chest radiographs, and respiratory function tests (RFT) were performed. A rheumatologist performed the lung US. High-resolution CT (HRCT) was also performed. The patients were followed every 12 weeks for 48 weeks. Results: A total of 79 of 133 patients (59.4%) showed US signs of ILD in contrast to healthy controls (4.8%) (p = 0.0001). Anti-centromere antibodies (p = 0.005) and RSS (p = 0.004) showed an association with ILD. A positive correlation was demonstrated between the US and HRCT findings (p = 0.001). The sensitivity and specificity of US in detecting ILD were 91.2% and 88.6%, respectively. In the follow-up, a total of 30 patients out of 79 (37.9%) who demonstrated US signs of ILD at baseline, showed changes in the ILD score by US. Conclusions: US showed a high prevalence of subclinical ILD in SSc patients. It proved to be a valid, reliable, and feasible tool to detect ILD in SSc and to monitor disease progression.
Full article
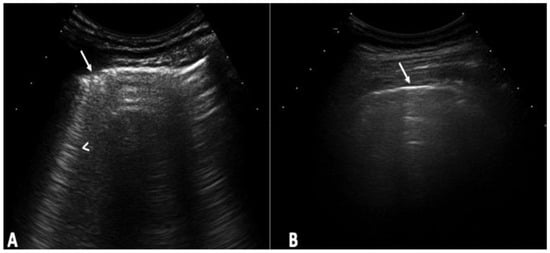
Figure 1
Open AccessRetraction
RETRACTED: Nobel et al. Modern Subtype Classification and Outlier Detection Using the Attention Embedder to Transform Ovarian Cancer Diagnosis. Tomography 2024, 10, 105–132
by
S. M. Nuruzzaman Nobel, S M Masfequier Rahman Swapno, Md. Ashraful Hossain, Mejdl Safran, Sultan Alfarhood, Md. Mohsin Kabir and M. F. Mridha
Tomography 2024, 10(4), 520; https://doi.org/10.3390/tomography10040040 - 03 Apr 2024
Abstract
The Tomography Editorial Office retracts the article “Modern Subtype Classification and Outlier Detection Using the Attention Embedder to Transform Ovarian Cancer Diagnosis” [...]
Full article
Open AccessArticle
Impact of Deep Learning Denoising Algorithm on Diffusion Tensor Imaging of the Growth Plate on Different Spatial Resolutions
by
Laura Santos, Hao-Yun Hsu, Ronald R. Nelson, Jr., Brendan Sullivan, Jaemin Shin, Maggie Fung, Marc R. Lebel, Sachin Jambawalikar and Diego Jaramillo
Tomography 2024, 10(4), 504-519; https://doi.org/10.3390/tomography10040039 - 02 Apr 2024
Abstract
To assess the impact of a deep learning (DL) denoising reconstruction algorithm applied to identical patient scans acquired with two different voxel dimensions, representing distinct spatial resolutions, this IRB-approved prospective study was conducted at a tertiary pediatric center in compliance with the Health
[...] Read more.
To assess the impact of a deep learning (DL) denoising reconstruction algorithm applied to identical patient scans acquired with two different voxel dimensions, representing distinct spatial resolutions, this IRB-approved prospective study was conducted at a tertiary pediatric center in compliance with the Health Insurance Portability and Accountability Act. A General Electric Signa Premier unit (GE Medical Systems, Milwaukee, WI) was employed to acquire two DTI (diffusion tensor imaging) sequences of the left knee on each child at 3T: an in-plane 2.0 × 2.0
(This article belongs to the Topic AI in Medical Imaging and Image Processing)
►▼
Show Figures
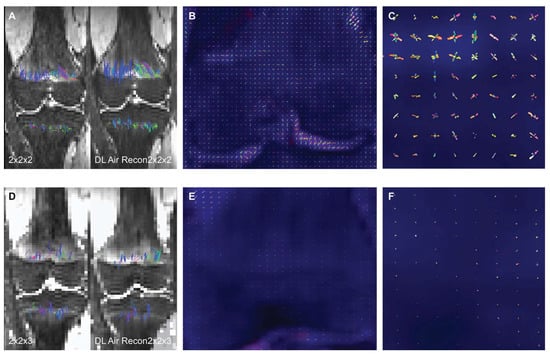
Figure 1
Open AccessArticle
Test–Retest Reproducibility of Reduced-Field-of-View Density-Weighted CRT MRSI at 3T
by
Nicholas Farley, Antonia Susnjar, Mark Chiew and Uzay E. Emir
Tomography 2024, 10(4), 493-503; https://doi.org/10.3390/tomography10040038 - 29 Mar 2024
Abstract
Quantifying an imaging modality’s ability to reproduce results is important for establishing its utility. In magnetic resonance spectroscopic imaging (MRSI), new acquisition protocols are regularly introduced which improve upon their precursors with respect to signal-to-noise ratio (SNR), total acquisition duration, and nominal voxel
[...] Read more.
Quantifying an imaging modality’s ability to reproduce results is important for establishing its utility. In magnetic resonance spectroscopic imaging (MRSI), new acquisition protocols are regularly introduced which improve upon their precursors with respect to signal-to-noise ratio (SNR), total acquisition duration, and nominal voxel resolution. This study has quantified the within-subject and between-subject reproducibility of one such new protocol (reduced-field-of-view density-weighted concentric ring trajectory (rFOV-DW-CRT) MRSI) by calculating the coefficient of variance of data acquired from a test–retest experiment. The posterior cingulate cortex (PCC) and the right superior corona radiata (SCR) were selected as the regions of interest (ROIs) for grey matter (GM) and white matter (WM), respectively. CVs for between-subject and within-subject were consistently around or below 15% for Glx, tCho, and Myo-Ins, and below 5% for tNAA and tCr.
Full article
(This article belongs to the Section Brain Imaging)
►▼
Show Figures
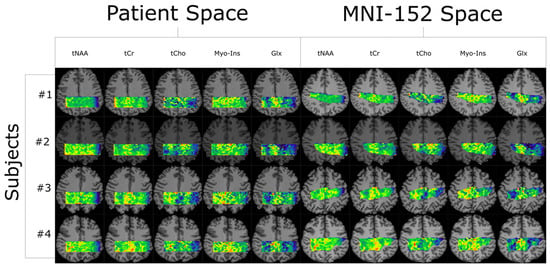
Figure 1
Open AccessArticle
Multifractal Analysis of Choroidal SDOCT Images in the Detection of Retinitis Pigmentosa
by
Francesca Minicucci, Fotios D. Oikonomou and Angela A. De Sanctis
Tomography 2024, 10(4), 480-492; https://doi.org/10.3390/tomography10040037 - 29 Mar 2024
Abstract
►▼
Show Figures
The aim of this paper is to investigate whether a multifractal analysis can be applied to study choroidal blood vessels and help ophthalmologists in the early diagnosis of retinitis pigmentosa (RP). In a case study, we used spectral domain optical coherence tomography (SDOCT),
[...] Read more.
The aim of this paper is to investigate whether a multifractal analysis can be applied to study choroidal blood vessels and help ophthalmologists in the early diagnosis of retinitis pigmentosa (RP). In a case study, we used spectral domain optical coherence tomography (SDOCT), which is a noninvasive and highly sensitive imaging technique of the retina and choroid. The image of a choroidal branching pattern can be regarded as a multifractal. Therefore, we calculated the generalized Renyi point-centered dimensions, which are considered a measure of the inhomogeneity of data, to prove that it increases in patients with RP as compared to those in the control group.
Full article
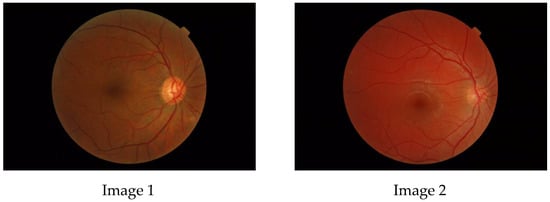
Figure 1
Open AccessArticle
Chronological Course and Clinical Features after Denver Peritoneovenous Shunt Placement in Decompensated Liver Cirrhosis
by
Shingo Koyama, Asako Nogami, Masato Yoneda, Shihyao Cheng, Yuya Koike, Yuka Takeuchi, Michihiro Iwaki, Takashi Kobayashi, Satoru Saito, Daisuke Utsunomiya and Atsushi Nakajima
Tomography 2024, 10(4), 471-479; https://doi.org/10.3390/tomography10040036 - 25 Mar 2024
Abstract
Background: Refractory ascites affects the prognosis and quality of life in patients with liver cirrhosis. Peritoneovenous shunt (PVS) is a treatment procedure of palliative interventional radiology for refractory ascites. Although it is reportedly associated with serious complications (e.g., heart failure, thrombotic disease), the
[...] Read more.
Background: Refractory ascites affects the prognosis and quality of life in patients with liver cirrhosis. Peritoneovenous shunt (PVS) is a treatment procedure of palliative interventional radiology for refractory ascites. Although it is reportedly associated with serious complications (e.g., heart failure, thrombotic disease), the clinical course of PVS has not been thoroughly evaluated. Objectives: To evaluate the relationship between chronological course and complications after PVS for refractory ascites in liver cirrhosis patients. Materials and Methods: This was a retrospective study of 14 patients with refractory ascites associated with decompensated cirrhosis who underwent PVS placement between June 2011 and June 2023. The clinical characteristics, changes in cardiothoracic ratio (CTR), and laboratory data (i.e., brain natriuretic peptide (BNP), D-dimer, platelet) were evaluated. Follow-up CT images in eight patients were also evaluated for ascites and complications. Results: No serious complication associated with the procedure occurred in any case. Transient increases in BNP and D-dimer levels, decreased platelet counts, and the worsening of CTR were observed in the 2 days after PVS; however, they were improved in 7 days in all cases except one. In the follow-up CT, the amount of ascites decreased in all patients, but one patient with a continuous increase in D-dimer 2 and 7 days after PVS had thrombotic disease (renal and splenic infarction). The mean PVS patency was 345.4 days, and the median survival after PVS placement was 474.4 days. Conclusions: PVS placement for refractory ascites is a technically feasible palliative therapy. The combined evaluation of chronological changes in BNP, D-dimer, platelet count and CTR, and follow-up CT images may be useful for the early prediction of the efficacy and complications of PVS.
Full article
(This article belongs to the Section Abdominal Imaging)
►▼
Show Figures
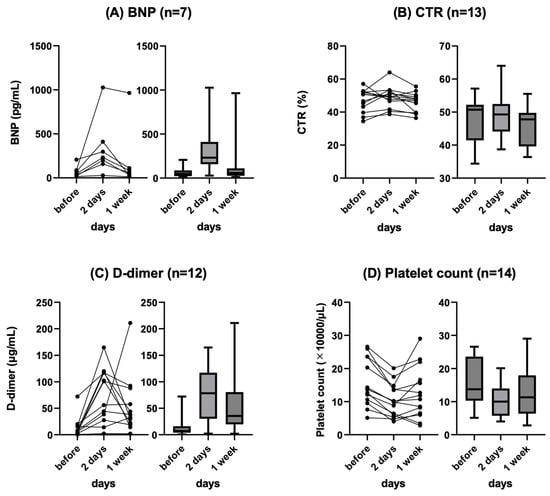
Figure 1
Open AccessArticle
Validation of Left Atrial Volume Correction for Single Plane Method on Four-Chamber Cine Cardiac MRI
by
Hosamadin Assadi, Nicholas Sawh, Ciara Bailey, Gareth Matthews, Rui Li, Ciaran Grafton-Clarke, Zia Mehmood, Bahman Kasmai, Peter P. Swoboda, Andrew J. Swift, Rob J. van der Geest and Pankaj Garg
Tomography 2024, 10(4), 459-470; https://doi.org/10.3390/tomography10040035 - 25 Mar 2024
Abstract
Background: Left atrial (LA) assessment is an important marker of adverse cardiovascular outcomes. Cardiovascular magnetic resonance (CMR) accurately quantifies LA volume and function based on biplane long-axis imaging. We aimed to validate single-plane-derived LA indices against the biplane method to simplify the post-processing
[...] Read more.
Background: Left atrial (LA) assessment is an important marker of adverse cardiovascular outcomes. Cardiovascular magnetic resonance (CMR) accurately quantifies LA volume and function based on biplane long-axis imaging. We aimed to validate single-plane-derived LA indices against the biplane method to simplify the post-processing of cine CMR. Methods: In this study, 100 patients from Leeds Teaching Hospitals were used as the derivation cohort. Bias correction for the single plane method was applied and subsequently validated in 79 subjects. Results: There were significant differences between the biplane and single plane mean LA maximum and minimum volumes and LA ejection fraction (EF) (all p < 0.01). After correcting for biases in the validation cohort, significant correlations in all LA indices were observed (0.89 to 0.98). The area under the curve (AUC) for the single plane to predict biplane cutoffs of LA maximum volume ≥ 112 mL was 0.97, LA minimum volume ≥ 44 mL was 0.99, LA stroke volume (SV) ≤ 21 mL was 1, and LA EF ≤ 46% was 1, (all p < 0.001). Conclusions: LA volumetric and functional assessment by the single plane method has a systematic bias compared to the biplane method. After bias correction, single plane LA volume and function are comparable to the biplane method.
Full article
(This article belongs to the Topic AI in Medical Imaging and Image Processing)
►▼
Show Figures
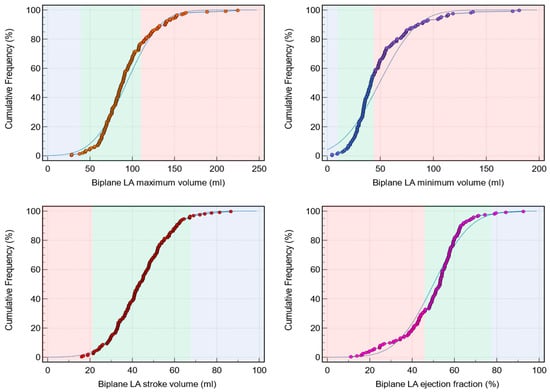
Figure 1
Open AccessArticle
Anatomy of Maxillary Sinus: Focus on Vascularization and Underwood Septa via 3D Imaging
by
Sara Bernardi, Serena Bianchi, Davide Gerardi, Pierpaolo Petrelli, Fabiola Rinaldi, Maurizio Piattelli, Guido Macchiarelli and Giuseppe Varvara
Tomography 2024, 10(4), 444-458; https://doi.org/10.3390/tomography10040034 - 24 Mar 2024
Abstract
►▼
Show Figures
The study of the maxillary sinus anatomy should consider the presence of two features of clinical importance. The arterial supply course and the presence of the so-called Underwood septa are two important factors to consider when planning surgical treatment to reduce the risk
[...] Read more.
The study of the maxillary sinus anatomy should consider the presence of two features of clinical importance. The arterial supply course and the presence of the so-called Underwood septa are two important factors to consider when planning surgical treatment to reduce the risk of surgical complications such as excessive bleeding and Schneiderian membrane perforations. This study aimed to investigate the above-mentioned anatomical structures to improve the management of eventual vascular and surgical complications in this area. This study included a total of 200 cone-beam computed topographies (CBCTs) divided into two groups of 100 CBCTs to evaluate the arterial supply (AAa) course through the lateral sinus wall and Underwood’s septa, respectively. The main parameters considered on 3D imaging were the presence of the AAa in the antral wall, the length of the arterial pathway, the height of the maxillary bone crest, the branch sizes of the artery in the first group, and the position of the septa, the length of the septa, and their gender associations in the second group. The CBCT analysis showed the presence of the arterial supply through the bone wall in 100% of the examined patients, with an average size of 1.07 mm. With regard to the septa, 19% of patients presented variations, and no gender difference was found to be statistically significant. The findings add to the current understanding of the clinical structure of the maxillary sinus, equipping medical professionals with vital details for surgical preparation and prevention of possible complications.
Full article
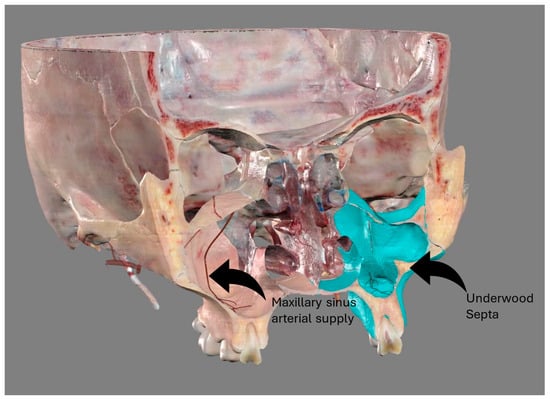
Figure 1
Open AccessArticle
The Utility of Spectroscopic MRI in Stereotactic Biopsy and Radiotherapy Guidance in Newly Diagnosed Glioblastoma
by
Abinand C. Rejimon, Karthik K. Ramesh, Anuradha G. Trivedi, Vicki Huang, Eduard Schreibmann, Brent D. Weinberg, Lawrence R. Kleinberg, Hui-Kuo G. Shu, Hyunsuk Shim and Jeffrey J. Olson
Tomography 2024, 10(3), 428-443; https://doi.org/10.3390/tomography10030033 - 20 Mar 2024
Abstract
Current diagnostic and therapeutic approaches for gliomas have limitations hindering survival outcomes. We propose spectroscopic magnetic resonance imaging as an adjunct to standard MRI to bridge these gaps. Spectroscopic MRI is a volumetric MRI technique capable of identifying tumor infiltration based on its
[...] Read more.
Current diagnostic and therapeutic approaches for gliomas have limitations hindering survival outcomes. We propose spectroscopic magnetic resonance imaging as an adjunct to standard MRI to bridge these gaps. Spectroscopic MRI is a volumetric MRI technique capable of identifying tumor infiltration based on its elevated choline (Cho) and decreased N-acetylaspartate (NAA). We present the clinical translatability of spectroscopic imaging with a Cho/NAA ≥ 5x threshold for delineating a biopsy target in a patient diagnosed with non-enhancing glioma. Then, we describe the relationship between the undertreated tumor detected with metabolite imaging and overall survival (OS) from a pilot study of newly diagnosed GBM patients treated with belinostat and chemoradiation. Each cohort (control and belinostat) were split into subgroups using the median difference between pre-radiotherapy Cho/NAA ≥ 2x and the treated T1-weighted contrast-enhanced (T1w-CE) volume. We used the Kaplan–Meier estimator to calculate median OS for each subgroup. The median OS was 14.4 months when the difference between Cho/NAA ≥ 2x and T1w-CE volumes was higher than the median compared with 34.3 months when this difference was lower than the median. The T1w-CE volumes were similar in both subgroups. We find that patients who had lower volumes of undertreated tumors detected via spectroscopy had better survival outcomes.
Full article
(This article belongs to the Special Issue Progress in the Use of Advanced Imaging for Radiation Oncology)
►▼
Show Figures
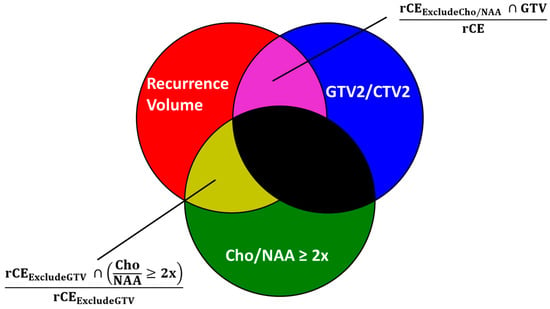
Figure 1
Open AccessReview
CT Arthrography of the Elbow: What Radiologists Should Know
by
Gianluca Folco, Carmelo Messina, Salvatore Gitto, Stefano Fusco, Francesca Serpi, Andrea Zagarella, Mauro Battista Gallazzi, Paolo Arrigoni, Alberto Aliprandi, Marco Porta, Paolo Vitali, Luca Maria Sconfienza and Domenico Albano
Tomography 2024, 10(3), 415-427; https://doi.org/10.3390/tomography10030032 - 11 Mar 2024
Abstract
Computed tomography (CT) arthrography is a quickly available imaging modality to investigate elbow disorders. Its excellent spatial resolution enables the detection of subtle pathologic changes of intra-articular structures, which makes this technique extremely valuable in a joint with very tiny chondral layers and
[...] Read more.
Computed tomography (CT) arthrography is a quickly available imaging modality to investigate elbow disorders. Its excellent spatial resolution enables the detection of subtle pathologic changes of intra-articular structures, which makes this technique extremely valuable in a joint with very tiny chondral layers and complex anatomy of articular capsule and ligaments. Radiation exposure has been widely decreased with the novel CT scanners, thereby increasing the indications of this examination. The main applications of CT arthrography of the elbow are the evaluation of capsule, ligaments, and osteochondral lesions in both the settings of acute trauma, degenerative changes, and chronic injury due to repeated microtrauma and overuse. In this review, we discuss the normal anatomic findings, technical tips for injection and image acquisition, and pathologic findings that can be encountered in CT arthrography of the elbow, shedding light on its role in the diagnosis and management of different orthopedic conditions. We aspire to offer a roadmap for the integration of elbow CT arthrography into routine clinical practice, fostering improved patient outcomes and a deeper understanding of elbow pathologies.
Full article
(This article belongs to the Special Issue CT Arthrography)
►▼
Show Figures
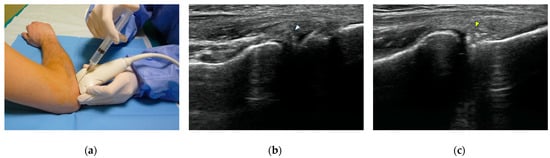
Figure 1
Open AccessArticle
Photon Counting Computed Tomography for Accurate Cribriform Plate (Lamina Cribrosa) Imaging in Adult Patients
by
Anna Klempka, Eduardo Ackermann, Sven Clausen and Christoph Groden
Tomography 2024, 10(3), 400-414; https://doi.org/10.3390/tomography10030031 - 08 Mar 2024
Abstract
Detailed visualization of the cribriform plate is challenging due to its intricate structure. This study investigates how computed tomography (CT) with a novel photon counting (PC) detector enhance cribriform plate visualization compared to traditionally used energy-integrated detectors in patients. A total of 40
[...] Read more.
Detailed visualization of the cribriform plate is challenging due to its intricate structure. This study investigates how computed tomography (CT) with a novel photon counting (PC) detector enhance cribriform plate visualization compared to traditionally used energy-integrated detectors in patients. A total of 40 patients were included in a retrospective analysis, with half of them undergoing PC CT (Naeotom Alpha Siemens Healthineers, Forchheim, Germany) and the other half undergoing CT scans using an energy-integrated detector (Somatom Sensation 64, Siemens, Forchheim, Germany) in which the cribriform plate was visualized with a temporal bone protocol. Both groups of scans were evaluated for signal-to-noise ratio, radiation dose, the imaging quality of the whole scan overall, and, separately, the cribriform plate and the clarity of volume rendering reconstructions. Two independent observers conducted a qualitative analysis using a Likert scale. The results consistently demonstrated excellent imaging of the cribriform plate with the PC CT scanner, surpassing traditional technology. The visualization provided by PC CT allowed for precise anatomical assessment of the cribriform plate on multiplanar reconstructions and volume rendering imaging with reduced radiation dose (by approximately 50% per slice) and higher signal-to-noise ratio (by approximately 75%). In conclusion, photon-counting technology provides the possibility of better imaging of the cribriform plate in adult patients. This enhanced imaging could be utilized in skull base-associated pathologies, such as cerebrospinal fluid leaks, to visualize them more reliably for precise treatment.
Full article
(This article belongs to the Section Neuroimaging)
►▼
Show Figures
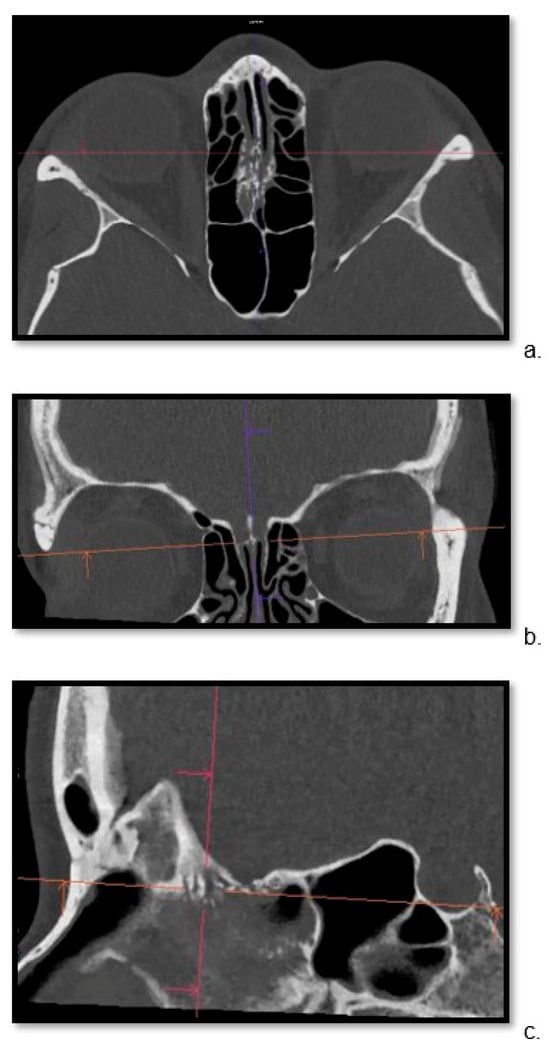
Figure 1
Highly Accessed Articles
Latest Books
E-Mail Alert
News
Topics
Topic in
Anatomia, Biology, Medicina, Pathophysiology, Tomography
Human Anatomy and Pathophysiology, 2nd Volume
Topic Editors: Francesco Cappello, Mugurel Constantin RusuDeadline: 31 May 2024
Topic in
Applied Sciences, Cancers, Diagnostics, Tomography
Deep Learning for Medical Image Analysis and Medical Natural Language Processing
Topic Editors: Mizuho Nishio, Koji FujimotoDeadline: 20 November 2024
Topic in
BioMed, Cancers, Diagnostics, JCM, Tomography
AI in Medical Imaging and Image Processing
Topic Editors: Karolina Nurzynska, Michał Strzelecki, Adam Piórkowski, Rafał ObuchowiczDeadline: 31 December 2024
Topic in
Diagnostics, JCTO, JCM, JPM, Tomography
Optical Coherence Tomography (OCT) and OCT Angiography – Recent Advances
Topic Editors: Sumit Randhir Singh, Jay ChhablaniDeadline: 26 May 2025

Conferences
Special Issues
Special Issue in
Tomography
Breakthroughs in Breast Radiology
Guest Editor: Matthew A. LewisDeadline: 15 May 2024
Special Issue in
Tomography
Innovative Approaches in Neuronal Imaging and Mental Health
Guest Editors: Fernando Ferreira-Santos, Miguel Castelo-BrancoDeadline: 30 June 2024
Special Issue in
Tomography
Novel Imaging Advances in Physiotherapy
Guest Editor: Juan Antonio Valera-CaleroDeadline: 12 July 2024
Special Issue in
Tomography
Functional and Molecular Imaging of the Abdomen
Guest Editor: Michael T. McMahonDeadline: 31 July 2024